3.   Generating Functions


This chapter introduces a central concept in the analysis of algorithms and in combinatorics: generating functions — a necessary and natural link between the algorithms that are our objects of study and analytic methods that are necessary to discover their properties.


3.1 Ordinary Generating Functions

Often, our goal in the analysis of algorithms is to derive specific expressions for the values of terms in a sequence of quantities $a_0, a_1, a_2, \ldots$ that measure some performance parameter. In this chapter we see the benefits of working with a single mathematical object that represents the whole sequence.

Definition. Given a sequence $a_0, a_1, a_2, \ldots, a_k, \ldots$, the function $$A(z)=\sum_{k\ge0}a_k z^k$$ is called the ordinary generating function (OGF) of the sequence. We use the notation $[z^k]A(z)$ to refer to the coefficient $a_k$.


Sequence OGF
$$1,\,1,\,1,\,1,\,\ldots,\,1,\,\ldots$$ $${1\over 1-z}=\sum_{N\ge0}z^N$$
$$0,\,1,\,2,\,3,\,4,\,\ldots,\,N,\,\ldots$$ $${z\over(1-z)^2}=\sum_{N\ge1}Nz^N$$
$$0,\,0,\,1,\,3,\,6,\,10,\,\ldots,\,{N\choose2},\,\ldots$$ $${z^2\over(1-z)^3}=\sum_{N\ge2}{N\choose2}z^N$$
$$0,\,\ldots,\,0,\,1,\,M+1,\,\ldots,\,{N\choose M},\,\ldots$$ $${z^M\over(1-z)^{M+1}}=\sum_{N\ge M}{N\choose M}z^N$$
$$1,\,M,\,{M\choose 2}\,\ldots,\,{M\choose N},\,\ldots,\,M,\,1$$ $${(1+z)^M}=\sum_{N\ge0}{M\choose N}z^N$$
$$1,\,M+1,\,{M+2\choose2},\,{M+3\choose3},\,\ldots$$ $${1\over(1-z)^{M+1}}=\sum_{N\ge 0}{N+M\choose N}z^N$$
$$1,\,0,\,1,\,0,\,\ldots,\,1,\,0,\,\ldots$$ $${1\over 1-z^2}=\sum_{N\ge0}z^{2N}$$
$$1,\,c,\,c^2,\,c^3,\,\ldots,\,c^N,\,\ldots$$ $${1\over1-cz}=\sum_{N\ge0}c^Nz^N$$
$$1,\,1,\,{1\over2!},\,{1\over3!},\,{1\over4!},\,\ldots,\,{1\over N!},\,\ldots$$ $$e^z=\sum_{N\ge0}{\displaystyle z^N\over N!}$$
$$0,\,1,\,{1\over2},\,{1\over3},\,{1\over4},\,\ldots,\,{1\over N},\,\ldots$$ $$\ln{1\over1-z}=\sum_{N\ge1}{\displaystyle z^N\over N}$$
$$0,\,1,\,1+{1\over2},\,1+{1\over2}+{1\over3},\,\ldots,\,H_N,\,\ldots$$ $${1\over1-z}\ln{1\over1-z}=\sum_{N\ge1}H_Nz^N$$
$$0,\,0,\,1,\,3({1\over2}+{1\over3}),\,4({1\over2}+{1\over3}+{1\over4}),\,\ldots$$ $${z\over(1-z)^2}\ln{1\over1-z}=\sum_{N\ge0}N(H_N-1)z^N$$


Given generating functions $A(z)=\sum_{k\ge0}a_kz^k$ and $B(z)=\sum_{k\ge0}b_kz^k$ that represent the sequences $a_0,a_1,\ldots,a_k,\ldots$ and $b_0,b_1,\ldots,b_k,\ldots$, we can perform a number of simple transformations to get generating functions for other sequences.


Operation Result
right shift $$zA(z)=\sum_{n\ge1}a_{n-1}z^n$$
left shift $${A(z)-a_0\over z}=\sum_{n\ge0}a_{n+1}z^n$$
index multiply (differentiation) $$A^\prime(z)=\sum_{n\ge0}(n+1)a_{n+1}z^n$$
index divide (integration) $$\int_0^zA(t)dt=\sum_{n\ge1}{a_{n-1}\over n}z^n$$
scaling $$A(\lambda z)=\sum_{n\ge0}\lambda^na_nz^n$$
addition $$A(z)+B(z)=\sum_{n\ge0}(a_n+b_n)z^n$$
difference $${(1-z)A(z)}=a_0+\sum_{n\ge1}(a_n-a_{n-1})z^n$$
convolution $${A(z)B(z)}=\sum_{n\ge0}\Bigl(\,\sum_{0\le k\le n}a_kb_{n-k}\Bigr)z^n$$
partial sum $${A(z)\over1-z}=\sum_{n\ge0}\Bigl(\,\sum_{0\le k\le n}a_k\Bigr)z^n$$


3.2 Exponential Generating Functions

Some sequences are more conveniently handled by a generating function that involves a normalizing factor:

Definition. Given a sequence $a_0, a_1, a_2, \ldots, a_k, \ldots$, the function $$A(z)=\sum_{k\ge0}a_k {z^k\over k!}$$ is called the exponential generating function (EGF) of the sequence. We use the notation $k![z^k]A(z)$ to refer to the coefficient $a_k$.


Sequence EGF
$$1,\,1,\,1,\,1,\,\ldots,\,1,\,\ldots$$ $$e^z=\sum_{N\ge0}{z^N\over N!}$$
$$0,\,1,\,2,\,3,\,4,\,\ldots,\,N,\,\ldots$$ $$ze^z=\sum_{N\ge1}{z^N\over(N-1)!}$$
$$0,\,0,\,1,\,3,\,6,\,10,\,\ldots,\,{N\choose2},\,\ldots$$ $${1\over2}z^2e^z={1\over2}\sum_{N\ge2}{z^N\over(N-2)!}$$
$$\qquad0,\,\ldots,\,0,\,1,\,M+1,\,\ldots,\,{N\choose M},\,\ldots\qquad$$ $${1\over M!}z^Me^z={1\over M!}\sum_{N\ge M}{z^N\over(N-M)!}$$
$$1,\,0,\,1,\,0,\,\ldots,\,1,\,0,\,\ldots$$ $$\qquad{1\over2}(e^z+e^{-z})=\sum_{N\ge0}{1+(-1)^N\over2}{z^{N}\over N!}\qquad$$
$$1,\,c,\,c^2,\,c^3,\,\ldots,\,c^N,\,\ldots$$ $$e^{cz}=\sum_{N\ge0}{c^Nz^N\over N!}$$
$$0,\,1,\,{1\over2},\,{1\over3},\,\ldots,\,{1\over N+1},\,\ldots$$ $${\displaystyle e^z-1\over z}=\sum_{N\ge0}{\displaystyle z^N\over (N+1)!}$$
$$1,\,2,\,6,\,24,\,\ldots,\,N!,\,\ldots$$ $${\displaystyle 1\over 1-z}=\sum_{N\ge0}{\displaystyle N!z^N\over N!}$$


As with OGFs, application simple operations on these basic functions yields a large fraction of the EGFs that arise in practice. Note that the shift left/right operations for EGFs are the same as the index multiply/divide operations for OGFs and vice versa.


Operation Result
right shift (integration) $$\int_0^zA(t)dt=\sum_{n\ge1}a_{n-1}{z^n\over n!}$$
  left shift (differentiation)   $$A^\prime(z)=\sum_{n\ge0}a_{n+1}{z^n\over n!}$$
index multiply $$zA(z)=\sum_{n\ge0}na_{n-1}{z^n\over n!}$$
index divide $$(A(z)-A(0))/z=\sum_{n\ge1}{a_{n+1}\over n+1}{z^n\over n!}$$
addition $$A(z)+B(z)=\sum_{n\ge0}(a_n+b_n){z^n\over n!}$$
difference $$A^\prime(z)-A(z)=\sum_{n\ge0}(a_{n+1}-a_n){z^n\over n!}$$
binomial convolution $$\qquad{A(z)B(z)}=\sum_{n\ge0}\biggl(\>\sum_{0\le k\le n}{n\choose k}a_kb_{n-k}\biggr){z^n\over n!}\qquad$$
binomial sum $$e^zA(z)=\sum_{n\ge0}\biggl(\>\sum_{0\le k\le n}{n\choose k}a_k\biggr){z^n\over n!}$$


3.3 Generating Function Solution of Recurrences

Generating functions provide a mechanical method for solving many recurrence relations. Given a recurrence describing some sequence $\{a_n\}_{n\ge0}$, we can often develop a solution by carrying out the following steps:

The same method applies for EGFs, where we multiply by $z^n/n!$ and sum on $n$ in the first step. Whether OGFs or EGFs are more convenient depends on the recurrence.

Example. $$a_n=5a_{n-1}-6a_{n-2}\qquad\hbox{for $n>1$ with $a_0=0$ and $a_1=1$}$$ Use the generating function $a(z)=\sum_{n\ge0}a_nz^n$. Multiply both sides of the recurrence by $z^n$ and sum on $n$ to get the equation $$a(z)={z\over 1-5z+6z^2}={z\over(1-3z)(1-2z)}={1\over 1-3z}-{1\over 1-2z}$$ (by partial fractions) so that we must have $a_n=3^n-2^n$.

In general, we can solve a linear recurrence $$a_n=x_1a_{n-1}+x_2a_{n-2}+\ldots+x_ta_{n-t}$$ by expressing the generating function $a(z)$ as a rational function $f(z)/g(z)$ and then expanding:

Note that roots may be complex.

Example. $$a_n=2a_{n-1}-a_{n-2}+2a_{n-3}\qquad \hbox{for $n>2$ with $a_0=1$, $a_1=0$, and $a_2=-1$}.$$ This gives $$g(z)=1-2z+z^2-2z^3=(1+z^2)(1-2z)$$ and $$f(z)=(1-z^4)(1-2z)\pmod{z^4}=(1-2z),$$ so $$a(z)={f(z)\over g(z)}={1\over1+z^2}={1\over2}\Bigl({1\over1-iz}-{1\over1+iz}\Bigr),$$ and $a_n={1\over2}(i^n+(-i)^n)$. Thus, $a_n$ is $0$ for $n$ odd, $1$ when $n$ is a multiple of $4$, and $-1$ when $n$ is even but not a multiple of $4$ (this also follows directly from the form $a(z)=1/(1+z^2)$). For the initial conditions $a_0=1$, $a_1=2$, and $a_2=3$, we get $f(z)=1$, so the solution grows like $2^n$, but with periodic varying terms caused by the complex roots.


3.4 Expanding Generating Functions.

Given an explicit functional form for a generating function, we would like a general mechanism for finding the associated sequence. This process is called "expanding" the generating function, as we take it from a compact functional form into an infinite series of terms. Many functions are easily handled with a combination of Taylor's theorem $$f(z)=f(0)+f^{\prime}(0)z+{f^{\prime\prime}(0)\over2!}z^2 +{f^{\prime\prime\prime}(0)\over 3!}z^3 +{f^{\prime\prime\prime\prime}(0)\over 4!}z^4+\ldots.$$ and algebraic manipulations involving the basic identities and transformations given in the tables above. For more complicated functions, the theory of analytic combinatorics allows us to develop approximations to coefficients without expanding.


3.5 Transformations with Generating Functions


3.6 Functional Equations on Generating Functions


3.7 Solving the Quicksort Median-of-Three Recurrence with OGFs


3.8 Counting with Generating Functions

Generating functions provide a systematic way to count combinatorial objects. To illustrate, we consider a classical combinatorial problem that also corresponds to a fundamental data structure that will be considered in Chapter 5 and in several other places in the book. A binary tree is a structure defined recursively to be either a single external node or an internal node that is connected to two binary trees, a left subtree and a right subtree. Binary trees appear in many problems in combinatorics and the analysis of algorithms: for example, if internal nodes correspond to two-argument arithmetic operators and external nodes correspond to variables, then binary trees correspond to arithmetic expressions. The question at hand is, how many binary trees are there with $N$ external nodes?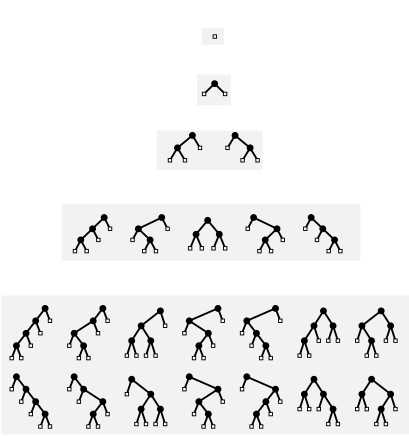


Counting binary trees (with a recurrence). Let $T_N$ be the number of binary trees with $N+1$ external nodes: $T_0=1$, $T_1=1$, $T_2=2$, $T_3=5$, and $T_4=14$. If the left subtree in a binary tree with $N+1$ external nodes has $k$ external nodes (there are $T_{k-1}$ different such trees), then the right subtree must have $N-k+1$ external nodes (there are $T_{N-k}$ possibilities), so $T_N$ must satisfy $$T_N = \sum_{1\le k\le N}T_{k-1}T_{N-k} \qquad\hbox{for $N>0$ with $T_0=1$}.$$ Multiplying by $z^N$ and summing on $N$ gives the nonlinear functional equation $$T(z)=zT(z)^2+1.$$ which is easily solved with the quadratic equation: $$zT(z)={1\over2}(1\pm\sqrt{1-4z}).$$ To get equality when $z=0$, we take the solution with a minus sign. To extract coefficients, use the binomial theorem with exponent $1\over2$ (Newton's formula): $$zT(z)=-{1\over2}\sum_{N\ge1}{{1\over2}\choose N}(-4z)^N.$$ Setting coefficients equal gives $$\eqalign{T_N&=-{1\over2}{{1\over2}\choose N+1}(-4)^{N+1}\cr &=-{1\over2}{{1\over2}({1\over2}-1)({1\over2}-2)\ldots({1\over2}-N)(-4)^{N+1}\over (N+1)!}\cr &={1\cdot 3\cdot 5\cdots(2N-1)\cdot2^{N}\over (N+1)!}\cr &={1\over N+1}{1\cdot 3\cdot 5\cdots(2N-1)\over N!}\, {2\cdot 4\cdot 6\cdots2N\over1\cdot 2\cdot 3\,\cdots\,N\,}\cr &={1\over N+1}{2N\choose N}.\cr}$$

These numbers are known as the Catalan numbers. In the next chapter, we will see that the approximate value is $T_{N}\approx 4^N/N\sqrt{\pi N}$.

Counting binary trees (direct). Define ${\cal T}$ to be the set of all binary trees, and adopt the notation $|t|$ to represent, for $t\in{\cal T}$, the number of internal nodes in $t$. Then we have the following derivation: $$\eqalign{T(z)&=\sum_{t\in{\cal T}}z^{|t|}\cr &=1+\sum_{t_L\in{\cal T}}\sum_{t_R\in{\cal T}}z^{|t_L|+|t_R|+1}\cr &=1+zT(z)^2\cr}$$ The first line is an alternate way to express $T(z)$ from its definition. Each tree with exactly $k$ external nodes contributes exactly $1$ to the coefficient of $z^k$, so the coefficient of $z^k$ in the sum ``counts'' the number of trees with $k$ internal nodes. The second line follows from the recursive definition of binary trees: either a binary tree has no internal nodes (which accounts for the $1$), or it can be decomposed into two independent binary trees whose internal nodes comprise the internal nodes of the original tree, plus one for the root. The third line follows because the index variables $t_L$ and $t_R$ are independent. Study this fundamental example carefully as it is the "poster child" for the general framework that we consider next.


3.9 The Symbolic Method

The symbolic method is a powerful approach for translating formal definitions of combinatorial objects into functional equations on generating functions.

Unlabelled objects. When counting with generating functions, we are considering classes of combinatorial objects, with a notion of "size" defined for each object. For a class $\cal A$, we denote the number of members of the class of size $n$ by $a_n$. Then we are interested in the OGF $$A(z)=\sum_{n\ge 0}a_nz^n=\sum_{a\in\cal A}z^{|a|}.$$ Given two classes $\cal A$ and $\cal B$ of combinatorial objects, we can combine them with a disjoint union operation $\cal A +\cal B$ that gives the class consisting of disjoint copies of the members of $\cal A$ and $\cal B$, by a Cartesian product operation $\cal A \times\cal B$ that gives the class of ordered pairs of objects (one from $\cal A$ and one from $\cal B$), and by a sequence operation that gives the class of sequences of objects from $\cal A$. These constructive definitions lead directly to the following functional relationships on the generating functions $A(z)$ and $B(z)$.

Building blocks.Combinatorial constructions ultimately emanate from these starting points:

Symbolic equations combining these with symbolic class names using disjoint union, Cartesian product, sequence, and other operations translate directly to functional equations on generating functions.

Example. Let $\cal G$ be the class of binary strings with no two consecutive $0$ bits. Such strings are either $\epsilon$, a single $0$, or $1$ or $01$ followed by a string with no two consecutive $0$ bits. Symbolically, $${\cal G} = \epsilon + \{0\} + \{1, 01\}\times{\cal G}.$$ Thus $$G(z) = 1 + z + (z + z^2)G(z).$$ and we have $G(z)=(1+z)/(1-z-z^2)$, which leads directly to the result that the number of strings of length $N$ with no two consecutive $0$ bits is $F_{N}+F_{N+1}=F_{N+2}$, a Fibonacci number.

Labelled objects. An alternative paradigm is to assume that the individual items {\it are} distinguishable---that they are {\it labelled} and that, therefore, the order in which items appear when assembled to make combinatorial objects is significant. Labelled objects are normally enumerated by exponential generating functions. For a labelled class $\cal A$, we are interested in the EGF $$A(z)=\sum_{n\ge 0}a_n{z^n\over n!}=\sum_{a\in\cal A}{z^{|a|}\over |a|!}.$$ When we combine two classes $\cal A$ and $\cal B$ of labelled objects, we need to relabel in a consistent manner so that only the labels $1$ to $N$ appear if the resulting object has size $N$. The disjoint union operation is essentially the same, but the product operation involves relabelling, so we use a different notation ($\cal A \star \cal B$). Again, the definitions lead directly to functional relationships on the generating functions.

See Chapter 6 for details and examples.


3.10 Lagrange Inversion.

The symbolic method makes it plain that we often are faced with extracting coefficients from generating functions that are implicitly defined through functional equations. The following general tool is available for this task, and is of particular importance in connection with tree enumeration.

Lagrange inversion theorem. If a generating function $A(z)=\sum_{n\ge0}a_nz^n$ satisfies the functional equation $z = f(A(z))$, where $f(z)$ satisfies $f(0)=0$ and $f^{\prime}(0)\ne0$, then $$a_n \equiv [z^n]A(z) = {1\over n}[u^{n-1}]\Bigl({u\over f(u)}\Bigr)^n.$$ Also, $$[z^n](A(z))^m = {m\over n}[u^{n-m}]\Bigl({u\over f(u)}\Bigr)^n.$$ and $$[z^n]g(A(z)) = {1\over n}[u^{n-1}]g^\prime(u)\Bigl({u\over f(u)}\Bigr)^n.$$

The functional inverse of a function $f$ is the function $f^{-1}$ that satisfies $f^{-1}(f(z))=f(f^{-1}(z))=z$. Applying $f^{-1}$ to both sides of the equation $z=f(A(z))$, we see that the function $A(z)$ is the functional inverse of $f(z)$. The Lagrange theorem is a general tool for inverting power series, in this sense. Its surprising feature is to provide a direct relation between the coefficients of the functional inverse of a function and the powers of that function.

Example. Let $T^{[2]}(z)=zT(z)$ be the OGF for binary trees, counted by external nodes. Rewriting the functional equation $T^{[2]}(z)=z+T^{[2]}(z)^2$ as $$z = T^{[2]}(z)-T^{[2]}(z)^2,$$ we can apply Lagrange inversion with $f(u)=u-u^2$. This gives the result $$[z^n]T^{[2]}(z) = {1\over n}[u^{n-1}]\Bigl({u\over u-u^2}\Bigr)^n = {1\over n}[u^{n-1}]\Bigl({1\over 1-u}\Bigr)^n.$$ Now, $${u^{n-1}\over(1-u)^n}=\sum_{k\ge n-1}{k\choose n-1}u^k$$ so that, considering the term $k=2n-2$, $$[u^{n-1}]\Bigl({1\over 1-u}\Bigr)^n = {2n-2\choose n-1} \quad\hbox{and therefore}\quad [z^n]T^{[2]}(z) = {1\over n}{2n-2\choose n-1},$$ as expected.


3.11 Probability Generating Functions


3.12 Bivariate Generating Functions


3.13 Special Functions



Generating functions have long been used in combinatorics, probability theory, and analytic number theory; hence a rich array of mathematical tools have been developed that turn out to be germane to the analysis of algorithms. We use generating functions both as combinatorial tools to aid in the process of precisely accounting for quantities of interest and as analytic tools to yield solutions. As such, their role in the analysis of algorithms is central.


Selected Exercises

3.1

Find the OGFs for each of the following sequences: $$\{2^{k+1}\}_{k\ge0}, \qquad\{k2^{k+1}\}_{k\ge0}, \qquad\{kH_k\}_{k\ge1}, \qquad\{k^3\}_{k\ge2}.$$


3.2

Find $[z^N]$ for each of the following OGFs: $${1\over(1-3z)^{4}}, \qquad(1- z)^2\ln{1\over1-z}, \qquad{1\over(1-2z^2)^2}.$$


3.4

Prove that $$\sum_{1\le k\le N}H_k = (N+1)(H_{N+1}-1).$$


3.6

Find the OGF for $$\Bigl\{\sum_{0< k< n}{1\over k(n-k)}\Bigr\}_{n>1}.$$


3.7

Find the OGF for $\{{H_k/k}\}_{k\ge1}$.


3.8

Find $[z^N]$ for each of the following OGFs: $$ {1\over1-z}\Bigl(\ln{1\over1-z}\Bigr)^2\qquad\hbox{and} \qquad\Bigl(\ln{1\over1-z}\Bigr)^3.$$ Use the notation $$H_N^{(2)}\equiv 1 + {1\over2^2} + {1\over3^2} + \ldots + {1\over N^2}$$ for the ``generalized harmonic numbers'' that arise in these expansions.


3.9

Find the EGFs for each of the following sequences: $$\{2^{k+1}\}_{k\ge0}, \qquad\{k2^{k+1}\}_{k\ge0}, \qquad\{k^3\}_{k\ge2}.$$


3.10

Find the EGFs for $1, 3, 5, 7, \ldots$ and $0, 2, 4, 6, \ldots$.


3.11

Find $N![z^N]A(z)$ for each of the following EGFs: $$A(z)={1\over 1-z}\ln{1\over 1-z}, \qquad A(z)=\Bigl(\ln{1\over 1-z}\Bigr)^2, \qquad A(z)=e^{z+z^2}.$$


3.16

Use generating functions to solve the following recurrences: $$\displaylines{ a_n = -a_{n-1} +6a_{n-2}\qquad\hbox{for $n>1$ with $a_0=0$ and $a_1=1$};\cr a_n = 11a_{n-2} -6a_{n-3}\qquad\hbox{for $n>2$ with $a_0=0$ and $a_1=a_2=1$};\cr a_n = 3a_{n-1} -4a_{n-2}\qquad\hbox{for $n>1$ with $a_0=0$ and $a_1=1$};\cr a_n = a_{n-1} -a_{n-2}\qquad\hbox{for $n>1$ with $a_0=0$ and $a_1=1$}.\cr }$$


3.17

Solve the recurrence $$a_n=5a_{n-1}-8a_{n-2}+4a_{n-3}\qquad\hbox{for $n>2$ with $a_0=1$, $a_1=2$, and $a_2=4$}.$$


3.18

Solve the recurrence $$a_n=2a_{n-2}-a_{n-4}\qquad\hbox{for $n>4$ with $a_0=a_1=0$ and $a_2=a_3=1$}.\ $$


3.19

Solve the recurrence $$a_n=6a_{n-1}-12a_{n-2}+18a_{n-3}-27a_{n-4}\quad\hbox{for $n>4$}$$ with $a_0=0$ and $a_1=a_2=a_3=1$.


3.20

Solve the recurrence $$a_n=3a_{n-1}-3a_{n-2}+a_{n-3}\quad\hbox{for $n>2$}$$ with $a_0=a_1=0$ and $a_2=1$. Solve the same recurrence with the initial condition on $a_1$ changed to $a_1=1$.


3.22

Use generating functions to solve the recurrence $$na_n = (n-2)a_{n-1} + 2\quad{\rm for}\ n>1{\rm \ with\ } a_1=1.$$


3.25

Use Taylor's theorem to find the expansions of the following functions: $$\sin(z),\qquad 2^z,\qquad ze^z.$$


3.27

Use Taylor's theorem to verify directly that $$H(z)={1\over1-z}\ln{1\over1-z}$$ is the generating function for the harmonic numbers.


3.28

Find an expression for $$[z^n]{1\over\sqrt{1-z}}\ln{1\over1-z}.$$ Hint. Expand $(1-z)^{-\alpha}$ and differentiate with respect to $\alpha$.


3.55

Discuss the form of an expression for $[z^N]D(z)$.


3.56

Write an efficient computer program that can compute $[z^N]D(z)$, given $N$.


3.58

[Euler] Show that $${1\over1-z}=(1+z)(1+z^2)(1+z^4)(1+z^8)\cdots.$$ Give a closed form for the product of the first $t$ factors. This identity is sometimes called the "computer scientist's identity." Why?


3.60

Express $[z^N](1-z)(1-z^2)(1-z^4)(1-z^8)\cdots$ in terms of the binary representation of $N$.


Review Questions

Q3.1

Suppose that $a_n$ satisfies $a_n = 9a_{n-1}-20a_{n-2} + n\quad{\rm for}\ n>1{\rm \ with\ } a_0=0 {\rm \ and\ } a_1=1 .$ What is $\lim_{n\to\infty}a_n/a_{n+1}$?


Q3.2

What is the value of $[z^n]\sum_{0\le k\le n}{2k\choose k}{2n-2k\choose n-k}$?


Q3.3

Do not use computer algebra for this question. Give the EGF of each of the following sequences:


   A. 0, -1, 1, -1, 1, -1, . . .


   B. 0, 1, 3, 7, 15, 31, 63, . . .


   C. 0, 1, 2, 3, 4, 5, 6, . . .


   D. 0, 1, 4, 9, 16, 25, 36, . . .


   E. 0, 1, 2, 6, 24, 120, 720, . . .


For each sequence, use one of the functions from this list: $(e^z-e^{-z})/2$, $ze^z$, $e^{2z}-e^z$, $(z^2+z)e^z$, $e^{-z}-1$, $z/(1-z)$, $e^{z^2}-1$.


Q3.4

(D. Carter) Find $[z^n]\bigl(1-{1\over z}\bigr)\ln(1-2z)$ for $n>0$.

Last modified on March 16, 2022.

Copyright © 1996–2020 Robert Sedgewick and Phillipe Flajolet. All rights reserved.